Source and Load Matching: Cyclist Perspective

If you ever ride a bicycle – you know how amazing that a bicycle with gear allow you to “match” your muscle (energy source) to any landscape (load). Essentially the gear match the source to load just like the way transformer match an AC source to its load.

Let’s look at a simplified diagram of the torque that your leg muscle generate versus the landscape – slope degree.



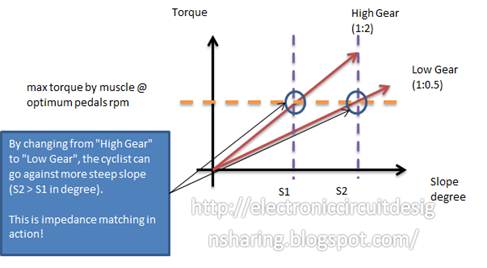
Assuming that at gear ratio of 1:1, for every turn of pedals the wheel will turn by one cycle, then:

Low Gear (1:0.5) means for every turns you make on the pedals, the wheel only make half a turn, since your leg muscle power is constant, your loss on speed is made up with your increase of forward force.

High Gear (1:2) means for every turns you make on the pedals, the wheel only make 2 turns, since your leg muscle power is constant  your gain on speed is made up with your reduction of forward force.

Now compare this to the impedance matching in audio amplifier:


Picture from Wikipedia - transformer to perform impedance matching

Source and Load Matching: DC perspective

Have you ever wonder why people talk about source and load matching? I did, and one thing that I asked my self is whether I have something in DC domain that can help me to visualized it. Well see below for my way of understanding source and load matching.

Supposed that we have a circuit as shown below:

From there we can create a table of maximum possible power that Rl can pull out of the source Vs:

Vs	Rs	Rl	Vo = VS * (Rl/(Rs+Rl))	Pout = (Vo^2)/Rl
1	1	0	0.00	-
1	1	0.2	0.17	0.14
1	1	0.4	0.29	0.20
1	1	0.6	0.38	0.23
1	1	0.8	0.44	0.25
1	1	1	0.50	0.25
1	1	1.2	0.55	0.25
1	1	1.4	0.58	0.24
1	1	1.6	0.62	0.24
1	1	1.8	0.64	0.23
1	1	2	0.67	0.22

From the table we can plot out the load power as Rl changes – as you can see, max Pout occurs when Rl “match” Rs, which is 1 Ohm in this example